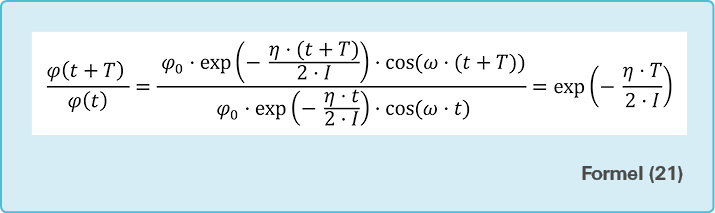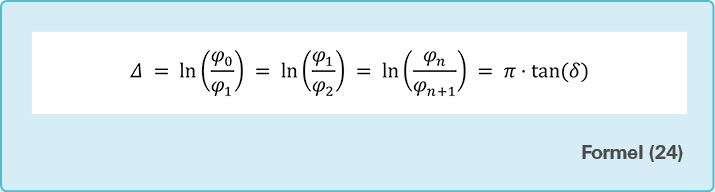Doping für die Fahrradreifen
Ein idealer Fahrradreifen weist einen niedrigen Rollwiderstand und eine hohe Haftreibung auf. Rennfahrer versuchen die Reifeneigenschaften durch eine Behandlung mit Essig zu verbessern. In dieser Arbeit wird auch eine Behandlung mit Styrol und Natriumsulfit durchgeführt. Messungen mit dem Torsionspendel zeigen, dass nach der Behandlung mit Styrol Verbesserungen sowohl beim Rollwiderstand als auch bei der Haftreibung zu erwarten sind.
1.1 Einleitung
Eine Grundbedingung für eine sichere Fortbewegung auf dem Fahrrad ist ein sicherer Kraftschluss der Reifen mit dem Bodenbelag. Dieser Kraftschluss ist nötig, um eine gute Kraftübertragung zu gewährleisten, insbesondere beim Beschleunigen, Bremsen oder Kurvenfahren. Ist dieser Kraftschluss nicht optimal, schafft vorsichtigeres Fahren zwar Abhilfe, bedeutet aber fast immer niedrigere Geschwindigkeiten, was gerade bei Rennfahrern nicht erwünscht ist.
Reifen, die ab Werk mit mehr Haftreibung ausgestattet sind, haben oftmals mehr Rollwiderstand. Dies wirkt sich wieder negativ auf die Gebrauchseigenschaften des Reifens aus. Deshalb kann man folgern, dass nur spezifische Verbesserungen am Equipment, respektive der Reifen, zentraler Angriffspunkt für entscheidende Optimierungen sein können.
1.2 Zielsetzung
In dieser Arbeit soll untersucht werden, ob die Performance von Fahrradreifen durch eine chemische Nachbehandlung verbessert werden kann. Es soll beantwortet werden, ob nur eine Optimierung für eine spezielle Situation sinnvoll ist oder ob der Reifen im Allgemeinen besser wird. Dies geschieht dabei in Bezug auf den Straßenrennsport nur mit Blick auf Rollwiderstand und Haftreibung. Die Nachbehandlung mit Natriumsulfit und Styrol werden theoretisch begründet. Während Essig getestet wird, weil diese Nachbehandlungsmethode ein weit verbreiteter Brauch unter Radfahrern ist. Dies soll mit leicht zugänglichen Mitteln bewerkstelligt werden.
Ein wesentlicher Aspekt der Arbeit ist die Entwicklung einer geeigneten Messmethode. Um eine möglichst gute Reproduzierbarkeit zu gewährleisten, wird darauf verzichtet, die Wirksamkeit der Nachbehandlung an irgendwelchen Rollenprüfständen oder auf der Straße zu testen, da der Einfluss von Umweltfaktoren schlecht eingewirkt werden kann und somit unter Umständen Veränderungen durch die Nachbehandlung selbst überdeckt werden könnten. Stattdessen wird das komplexe Schubmodul in einem Torsionspendel, dessen Torsionselement ein Stück der Lauffläche eines Reifens ist, und dessen Veränderungen durch die Nachbehandlung nachgewiesenen werden sollen, gemessen. Mittels bereits etablierter Modelle wird auf die Fahrperformance des Reifens geschlossen, was gerechtfertigt ist, weil Fokus der Arbeit die Untersuchung der chemischen und physikalischen Veränderungen im Polymer ist und nicht die Modellierung der Vorgänge im Reifen während der Fahrt. Zudem werden chemische Tests durchgeführt, um die eigentlichen Reaktionen an der Polymerstruktur direkt nachzuweisen.
2.1 Modellierung der Reifeneigenschaften mithilfe des komplexen Schubmoduls
Der temperaturabhängige, frequenzabhängige komplexe Schubmodul wird über eine sinusförmige Scherung definiert. Er ist das Verhältnis aus Scherspannung und Scherdeformation:
\(G\ast\;=\:\frac{\sigma\ast}{\gamma\ast}\) (1)
Die angelegte Deformation γ* kann durch die Gleichung (2) beschrieben werden. Um die Frequenzabhängigkeit gut darzustellen, wird angenommen, diese sei sinusförmig. Die sinusförmige Bewegung wird zur Vereinfachung nachfolgender Rechnungen als komplexe Größe dargestellt.
\(\gamma\ast\;(t)\;=\gamma_0\cdot e^{i\omega t}\) (2)
Dabei ist \(\gamma_0\) die Amplitude der Deformation, \(ω\) die Kreisfrequenz der periodischen Verformung \((\omega\;=\:2\;\cdot\;\pi\;\cdot\;f\;=\:\frac{2\pi}T)\), \(t\) die Zeit, i die imaginäre Einheit und e die Euler’sche Zahl. Die Deformation führt zu einer phasenverschobenen Spannung \(σ*\) im Material.
\(\sigma\ast\;(t)\;=\;\sigma_0\;\cdot\;e^{i(\omega t\;+\;\delta)}\) (3)
Hierbei ist \(σ_0\) die Amplitude der Spannung und \(δ\) der Phasenwinkel. Die restlichen Größen können aus Gleichung (2) entnommen werden. Die Deformationsamplitude bei einer Scherung gleicht dem Verhältnis aus maximaler Auslenkung \(l\) pro Probenhöhe \(h\).
\(\gamma_0\;=\:\frac lh\) (4)
Die Spannungsamplitude ist gegeben durch den Quotienten aus Kraft \(F\) pro Fläche \(A\) der Probe, die der Scherung unterworfen ist.
\(\sigma_0\;=\;\frac FA\) (5)
Substituiert man Gleichung (1) mit den Gleichungen (2) und (3) so erhält man nach dem Kürzen und Zusammenfassen folgende Gleichung.
\(G\ast\;=\:\frac{\sigma\ast}{\gamma\ast}\;=\:\frac{\sigma_0\;\cdot\;e^{i\omega t\;}}{\gamma_0\;\cdot\;e^{i\left(\omega t\;+\;\delta\right)}}\;=\:\frac{\sigma_0}{\gamma_0}\;\cdot\;e^{i\delta}\) (6)
Durch die Eulersche Identität \(e^{ix}\;=\;\cos(x)\;+\;\mathrm i\;\cdot\;\sin(x)\) lässt sich der Term in Realteil und Imaginärteil zerlegen.
Siehe Formel (7)

Der Realteil wird als Elastizitätsmodul \(G'\) bezeichnet. Dies ist ein Maß für die Energie, die elastisch aus der Verformung innerhalb eines Zyklus wiedergewonnen wird. Diese Eigenschaft kann mit einer Feder verglichen werden, die Energie ohne Verluste speichert und anschließend wieder abgibt.
\(G'\;=\:\frac{\sigma_0}{\gamma_0}\;\cdot\;\cos\left(\delta\right)\) (8)
Die durch den Realteil oder den Elastizitätsmodul verursachte rückstellende Kraft ist dabei in Phase mit der Auslenkung, gehorcht also im Wesentlichen dem Hooke’schen Gesetz.
Der Imaginärteil trägt den Namen Viskositätsmodul \(G''\).
\(G''\;=\:\frac{\sigma_0}{\gamma_0}\;\cdot\;\sin\left(\delta\right)\) (9)
Dieser ist dabei ein Maß für die Energie, die durch Wärme dissipiert wird. Die rückstellende Kraft ist hier nicht mehr proportional zur Auslenkung, sondern proportional zur Momentangeschwindigkeit, die um 90° phasenverschoben bezüglich der Auslenkung ist.
Bei der Überlagerung beider Moduln im Polymer ist also, wie in Gleichung (6) schon beschrieben, das Maximum der zurückstellenden Kraft, oder auch Spannung, zwischen 0° und 90° um den Winkel \(δ\) phasenverschoben. Eine Phasenverschiebung um 0° heißt völlig elastisch, vergleichbar mit einer idealen Feder, und 90° bedeutet, dass die Probe sich wie ein perfekter Dämpfer verhält, der die gesamte Energie einer Verformung in Wärme umwandelt.
Eine weitere wichtige Größe ist das Verhältnis beider Moduln. Dieses wird als Verlusttangens bezeichnet und leitet sich wie folgt her:
\(\frac{G''}{G'}\;=\:\frac{{\displaystyle\frac{\sigma_0}{\gamma_0}}\;\cdot\;\sin\left(\delta\right)}{\frac{\sigma_0}{\gamma_0}\;\cdot\;\cos\left(\delta\right)}\;=\:\frac{\displaystyle\sin\left(\delta\right)}{\;\cos\left(\delta\right)}\;=\:\tan\left(\delta\right)\) (10)
Die Korrelation des Schubmoduls mit den Reibwerten ist vielfältig und zunächst einmal durch die Frequenz bestimmt, wobei die Anregung des Reifens nicht monofrequent erfolgt, sondern simultan auf vielen verschiedenen Frequenzen [1, S. 28]. Betrachtet man den Rollwiderstand, so stellt man fest, dass die für ihn zutreffende Frequenz in der Größenordnung der Rotationsfrequenz des Laufrades liegt [1, S. 6 f.]. Hierbei gliedert sich der Rollwiderstand in zwei Komponenten auf [2, S. 51 ff.]. Die erste der beiden Komponenten ist der Walkwiderstand. Er ist ein Maß für die Energie, die verloren geht, wenn der Reifen vom Radius auf den dynamischen Radius pulsartig verformt wird. Dies lässt sich sehr gut durch eine sinusförmige Deformation in dem Frequenzbereich von 1 Hz bis 103 Hz modellieren. Je größer hier der Viskositätsmodul, beziehungsweise der Verlusttangens ist, desto größer ist der Teil der mechanischen Arbeit, die bei der Verformung aufgewandt wird und in Wärme umgewandelt wird. Da diese Wärme im Gegensatz zur mechanischen Arbeit nicht nutzbar ist, geht sie dem System verloren und verursacht den Walkwiderstand.
Andererseits beeinflusst nicht nur die Dämpfung, also Viskositätsmodul und Verlusttangens, das Rollverhalten des Reifens, sondern auch das Elastizitätsmodul trägt dazu bei. Wenn der Reifen unter Last ein wenig verformt wird, wird nicht mehr über den eigentlichen Berührpunkt abgerollt, sondern um eine etwas vorverlagerte Kippkante. Dieser vorverlagerte momentane Drehpunkt ist ähnlich wie bei der Fahrt auf einer Steigung [2, S. 53].
Die Bezeichnung, dass das Rad sich wie auf einer Steigung verhält, rührt daher, dass die Normalkraft etwas vor dem eigentlichen Berührpunkt, welcher direkt unter der Radachse liegt, angreift. Deshalb entsteht über die als Hebelarm wirkende Strecke \(\overrightarrow f\) in Kombination mit der Normalkraft ein der Bewegung entgegenwirkendes Drehmoment \(\overrightarrow{M}_R\;=\:\overrightarrow f\;\times\;\overrightarrow{F}_N\) um den Punkt \(D\). Bei idealem Rollen ohne Schlupf gleichen sich alle auf das Rad wirkenden Drehmomente betragsmäßig aus. Dabei wird das Gegendrehmoment \(\overrightarrow{M}_A\;=\:\overrightarrow r\;\times\;\overrightarrow{F}_A\;\approx\;\overrightarrow{r}_{dyn}\;\times\;\overrightarrow{F}_A\) durch die Vortriebskraft \(\overrightarrow{F}_A\) über den Radius \(\overrightarrow r\) oder eigentlich den dynamischen Radius \(\overrightarrow{r}_{dyn}\), der wegen der Verformung kleiner als der theoretische Radius ist, was jedoch im Allgemeinen vernachlässigbar ist, als Hebel erbracht. Betragsmäßig gilt:
\(F_A\;\cdot\;r\;=\:F_N\;\cdot\;f\) (11)
Da Kräftegleichgewicht herrscht, gilt, dass \(F_R\;=\:F_A\) und \(F_V\;=\:F_N\). Damit lässt sich Gleichung (11) substituieren, wobei \(F_R\) der Abrollwiderstand und \(F_N\) die Normalkraft ist.
\(F_R\;\cdot\;r\;=\:F_V\;\cdot\;f\) (12)
Löst man diese nach \(F_R\) auf, erhält man folgende Gleichung:
\(F_R\;=\:F_V\;\cdot\;\frac fr\) (13)
Dabei steigt \(f\) mit steigender Aufstandsfläche \(A\). Die Aufstandsfläche ist bei gleicher Radlast \(F_v\) umso größer, je kleiner der Betrag von \(G*\), also \(\sqrt{\left(G'\right)^2\;+\;\left(G'\right)^2}\), in dem Frequenzbereich unter 103 Hz ist. Denn das Schubmodul ist über einen konstanten Term, der die Poissonzahl \(ν\) enthält, direkt proportional zu dem Modul einer uniaxialen Dehnung \(E'\). Die Poissonzahl \(ν\) ist der Betrag des Verhältnisses aus relativer Querkontraktion zu Längskontraktion bei uniaxialer Dehnung und beträgt für alle isotropen, nichtkristallinen Materialien wie Gummi 0 ≤ ν ≤ 0,5. Zahlenmäßig gilt \(E'\;=\;2\;\cdot\;G'\;\cdot\;(1\;–\;\nu)\) und näherungsweise \(\vert E\ast\vert\;\leq\;3\;\cdot\;\vert G\ast\vert\) [1, S. 7; 3, S. 16; 4, S. 72]. Bei kleinerem Schubmodul ist also der Modul einer uniaxialen Dehnung kleiner und das Elastomer im Reifen wird bei gleicher Kraft oder Radlast \(F_v\) stärker komprimiert, weshalb die Aufstandsfläche \(A\) steigt. Dies heißt, dass der Hebelarm \(f\) größer ist und der dazu direkt proportionale Abrollwiderstand auch.
Wendet man den Blick von den makroskopischen Vorgängen zu den mikroskopischen Verformungen, so fällt auf, dass der Reifen nicht nur durch die wechselnde Radlast verformt wird, sondern bei immer auftretendem minimalem Schlupf auch von den auf der Straßenoberfläche vorkommenden Unebenheiten. Hier bewegt man sich typischerweise in einem Frequenzbereich von 103 bis 1010 Hz, wobei die Grenzen fließend sind. Höhere Gleitgeschwindigkeiten kommen einer Erhöhung der Frequenz gleich [1, S. 23]. Die hohen Frequenzen können einerseits dadurch erklärt werden, dass auch größere Unebenheiten sehr hohe Frequenzen anregen können. Gleitet der Reifen über eine herausstehende Unebenheit mit fast senkrechten Wänden, so wird der Gummi sehr schnell verdrängt. Die Deformation erfolgt hier pulsartig. Außerdem muss man sagen, dass es sich hier teilweise um empirische Daten [1, S. 23] handelt und die hohen Frequenzen vielleicht daher rühren, dass man den Verschiebungsfaktor bei der Erstellung von Masterkurven [1, S. 8] einfach als Frequenz angibt, ohne dass dies eine physikalisch interpretierbare Bedeutung hat.
Die Haftkraft eines Gummireifens setzt sich dabei aus Adhäsionskraft und Hysteresekraft zusammen:
\({\overset\rightharpoonup F}_R\;=\:{\overset\rightharpoonup F}_{Adh}\;+\;{\overset\rightharpoonup F}_{Hyst}\) (14)
Die Adhäsionskraft wird ausgemacht durch intermolekulare Wechselwirkungen zwischen Reifen und Fahrbahn. Sie ist damit abhängig von der wahren Kontaktfläche. Diese unterscheidet sich zur scheinbaren Aufstandsfläche dadurch, dass sie nicht den Teil der Aufstandsfläche beinhaltet, bei dem die beiden Reibpartner durch Unebenheiten oder einem Lubrikanten, wie Wasser oder Öl auf der Fahrbahn, voneinander getrennt sind. Die Hysteresekraft wird auch als Deformationskraft bezeichnet. Sie zeichnet sich dadurch aus, dass sich das Material, in diesem Fall der Gummi, beim Entlanggleiten an der Oberfläche dieser periodisch anpasst und somit periodisch deformiert wird. Beide Reibvorgänge haben eine Energiedissipation im Polymer zur Folge, was mit der Reibung oder Reibkraft gleichzusetzen ist [1, S. 9 ff.]. Je größer die Energiedissipation ist, desto mehr Kraft muss für den gleichen Weg bei geringfügigem Schlupf aufgebracht werden. Die Größe dieser Energiedissipation hängt vor allem mit dem Schubmodul zusammen. Laut Schramm [1] korreliert die Adhäsionskraft hier mit dem Betrag des Viskositätsmoduls \(G''\), während die Hysteresekraft abhängig vom Verlusttangens ist. Außerdem liegt die Hysteresekraft in einem tieferen Frequenzbereich als die Adhäsionskraft. Die Hysterese- beziehungsweise Adhäsionsreibung wird nur durch die unmittelbare Kontaktoberfläche bestimmt, da die für diesen Frequenzbereich zuständigen Deformationen des Reifens durch die Straße nur sehr kleine Amplituden in der Größenordnung von 2 μm besitzen [1, S. 62].
2.2 Einfluss der chemischen Struktur auf die viskoelastischen Materialeigenschaften
Bei einer Verformung werden die Polymerketten langgestreckt und somit parallel angeordnet. Dadurch wird die Entropie verringert. In der Relaxationsphase wird dieser Prozess umgekehrt. Das zweite Gesetz der Thermodynamik sagt aus, dass sich die Entropie wieder erhöhen muss und somit verkürzt sich das Polymer wieder, da es wieder in den ursprünglichen, ungeordneteren und entropiereicheren Knäuelzustand übergeht [5]. Die zwei entscheidenden Parameter sind dabei der Vernetzungsgrad N und die molare Masse M des Polymers, die als die Masse zwischen den Vernetzungspunkten definiert ist. Die Vernetzungspunkte können dabei auch temporäre Verhakungen der Polymerketten sein. Aktive Füllstoffe wie Ruß oder Kieselsäure binden die Polymerketten an sich und erzeugen somit weitere Knotenpunkte [6, S. 14 f.]. Der Elastizitätsmodul steht über folgende Gleichung mit diesen beiden Parametern in Verbindung.
\(G'\:=\:3\;\cdot\;N\:\cdot\;k\;\cdot\;T\;=\;\frac{3\;\cdot\;p}M\;\cdot\;R\;\cdot\;T\) (15)
Die restlichen Größen sind dabei die Temperatur T in Kelvin, die allgemeine Gaskonstante R, die Boltzmannkonstante k und die Dichte ρ [5]. Aus Gleichung (15) kann also entnommen werden, dass sowohl eine Erniedrigung des Vernetzungsgrades als auch eine Erhöhung der molaren Masse des Polymers zur Folge haben, dass der Elastizitätsmodul sinkt. Des Weiteren erwähnt Murayama [7, S. 81 ff.] qualitativ, dass die Dämpfung mit steigender molekularer Masse und Quervernetzung sinkt, wobei nur eine Veränderung bei der molekularen Masse hier zu einer verlässlichen Vorhersage oder Erklärung führen dürfte, da Veränderungen der Dämpfung durch die Quervernetzung stark vom Grad der Veränderung abhängen und unter Umständen das Gegenteil bewirken können. Die molekulare Masse, die mehr über die Masse der Seitenketten definiert wird, bezeichnet hierbei eine von der molaren Masse im Allgemeinen unterschiedliche Größe.
2.3 Gummi und seine chemischen Eigenschaften
In modernen Reifen werden komplexe und vielfältige Gummimischungen in der Lauffläche verwendet [8]. Dabei macht aus Naturkautschuk gewonnener Gummi einen großen Teil eines typischen Gummireifens aus. Gummi wird klassischerweise aus einer wässrigen Emulsion von Primärpolymeren (Latex) hergestellt. Die Primärpolymere bestehen aus Polyisoprenketten und besitzen Doppelbindungen als funktionelle Gruppen. Wird die Emulsion getrocknet, so besitzt der Stoff überwiegend plastische und kaum elastische Eigenschaften und ist für den Einsatz als Laufflächenmaterial ungeeignet.
Die Doppelbindungen jedoch ermöglichen es, dass der Kautschuk mit Hitze und Schwefel zu Gummi vulkanisiert werden kann, wobei Schwefelbrücken ausgebildet werden. Diese sind dabei ein bis vier Schwefelatome lang. Der komplette Reaktionsmechanismus ist noch nicht bekannt. Diese sogenannte Schwefelvulkanisation ist 1839 von Charles Goodyear entdeckt worden [9]. Bei der Vulkanisation von Naturkautschuken wird nach Gleichung (15) durch eine Erhöhung des Vernetzungsgrades der Elastizitätsmodul proportional dazu gesteigert.
Die zweite wichtige Komponente moderner Reifen ist Styrol-Butadienkautschuk [8], der dem Naturkautschuk chemisch sehr ähnlich ist [10]. Somit sind die Nachbehandlungen, die bei Naturkautschuk angewandt werden können, auch hier wirksam. Bei diesem sind ebenfalls Doppelbindungen abseits der aromatischen Doppelbindungen vorhanden und eine Schwefelvulkanisation kommt auch hier zum Einsatz [10].
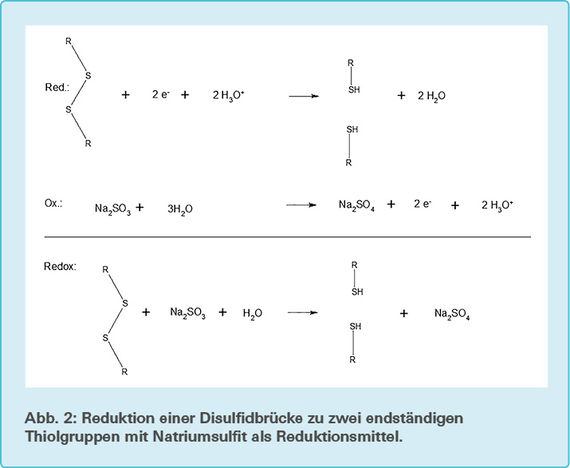
Die zwei wichtigsten Merkmale der beiden Kautschuke sind dabei die noch vorhandenen Doppelbindungen und die Schwefelbrücken. Da Reifen größtenteils aus diesen beiden Komponenten hergestellt werden, ist es möglich, diese beiden Strukturmerkmale für eine Nachbehandlung zu nutzen. Die Penetration des Gummis mit den Chemikalien durch natürliche Risse ist ausreichend, um signifikante Ergebnisse bei der Haftreibung zu erzielen, da nur die Veränderungen, auch Polarmodifikationen [11, S. 7] genannt, in der obersten Schicht eine Rolle spielen (vgl. 2.4). Die erste Möglichkeit der Polarmodifikation besteht darin, dass man durch ein geeignetes Reduktionsmittel die Schwefelbrücken zu Thiolgruppen reduziert (siehe Abb. 2).
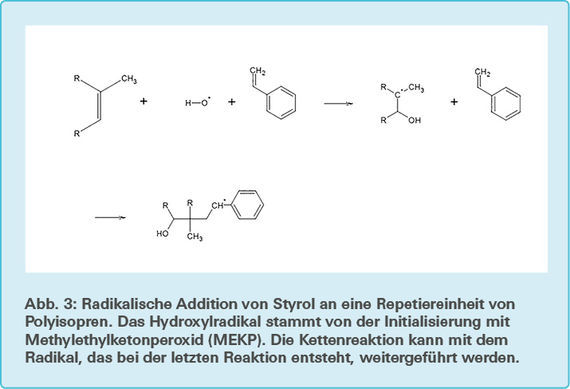
Dabei wird effektiv der Vernetzungsgrad gesenkt und die molare Masse zwischen zwei Vernetzungspunkten erhöht, wodurch man eine Erniedrigung des Elastizitätsmoduls erzielt. Zudem kann man auch die molare Masse des Gummis durch Zugabe eines weiteren Copolymers wie Styrol erhöhen. Dieses kann durch eine radikalische Addition in einer Kettenreaktion an das noch Doppelbindungen besitzende polymerisierte Primärpolymer im Gummi nach dem in Abb. 3 veranschaulichtem Mechanismus binden und hierdurch die molekulare und molare Masse erhöhen.
Andererseits besteht die Möglichkeit, dass das gebundene Styrol neue Querverbindungen bildet, die den Elastizitätsmodul erhöhen könnten. Auch ein höherer Grad an Verhakungen wäre möglich, da das Styrol potenziell mehr endständige Seitenketten erzeugen kann. Bei der Dämpfung wären zwei Veränderungen denkbar. Einerseits kann sie sinken, da die höhere Quervernetzung zu einer kleineren Dämpfung führt [7]. Andererseits können durch die neuen Querbrücken und vor allem die endständigen Seitenketten bei der Verformung mehr Verwerfungen und Spannungen im Polymer entstehen, was die Dämpfung erhöht. Die Bildung von Polystyrol, das ohne Bindung im Polymer ist, ist auch denkbar. Durch die gaschromatographische Analyse (vgl. 4.3) gibt es aber sehr starke Hinweise darauf, dass dies nicht der Fall ist.
Veränderungen des Polymers durch Alterungsprozesse werden in dieser Arbeit wegen des begrenzten Umfangs nicht betrachtet.
3.1 Theoretische Grundlagen
Das Torsionspendel stellt einen schwach gedämpften harmonischen Oszillator dar. Man kann mit den Anfangsbedindungen für \(t_0\;=\;0\;:\;\varphi\;=\;\varphi_0\) und \(\overset.\varphi\;=\;0\) folgende Differentialgleichung aufstellen.
\(I\;\cdot\;\overset{..}\varphi\;=\:-D\;\cdot\;\varphi\;-\;\eta\;\cdot\;\overset.\varphi\;\) (16)
In diesem Kontext ist \(I\) das Trägheitsmoment des Pendels, \(D\) das Direktionsmoment, \(η\) die Dämpfungskonstante, \(φ\) der momentane Auslenkungswinkel, \(\overset.\varphi\) die momentane Winkelgeschwindigkeit und \(\overset{..}\varphi\) die momentane Winkelbeschleunigung. Die Lösung dieser Gleichung sieht folgendermaßen aus:
\(\varphi\left(t\right)\;=\;\varphi_0\;\cdot\;exp\;\left(-\frac{\eta\;\cdot\;t}{2\;\cdot\;I}\right)\;\cdot\;\cos\left(\omega\;\cdot\;t\right)\) (17)
Die ursprüngliche, maximale Auslenkung ist dabei \(φ_0\), die Kreisfrequenz ist \(ω\). Sie ist bei einer Schwingung mit Dämpfung durch Gleichung (18) gegeben [12, S. 5 ff.].
\(\omega\;=\:\sqrt{\frac DI\;-\;\left(\frac\eta{2\;\cdot\;I}\right)^2}\) (18)
Da die Torsion in dem Pendel einer Scherung im Probenmaterial gleicht, hängt der Elastizitätsmodul direkt mit dem Direktionsmoment zusammen [3].
\(G'\;=\:\frac{l\;\cdot\;D}{I_T}\) (19)
Die Länge der quadratischen Probe wird dabei durch \(l\) und die Seitenlänge durch \(a\) repräsentiert. \(I_T\) ist dabei das Torsionsträgheitsmoment für eine Probe mit quadratischer Grundfläche, gegeben durch \(I_T = 0,141 \cdot\; a^4\) [13]. Löst man Gleichung 18 nach dem Direktionsmoment \(D\) auf und setzt dies in Gleichung 19 ein, erhält man Folgendes für den Elastizitätsmodul \(G'\):
\(G'\;=\:\frac{l\;\cdot\;\omega^2\;\cdot\;I\;+\;{\displaystyle\frac{l\;\cdot\;\eta^2}{4\;\cdot\;I}}}{0,141\;\cdot\;\alpha^4}\) (20)
Im Grenzwert \(η → 0\), also unter Vernachlässigung der Dämpfung, kommt auch Murayama [7, S. 43] auf das gleiche Ergebnis.
Da der Verlusttangens ein Maß dafür ist, wie viel Energie je Deformationszyklus als Wärme verloren geht beziehungsweise elastisch gespeichert ist, kann er über das Verhältnis der Amplituden hergeleitet werden. \(T\) ist dabei die Dauer einer Periode.
Siehe Formel (21)
Der Kosinus kann gekürzt werden, da er genau eine Periode später wieder beim gleichen Wert ist.
Bildet man von Gleichung 21 den natürlichen Logarithmus und den Betrag, so kommt man auf das logarithmische Dekrement \(Δ\).
\(Δ=\mathit\:\frac{\mathit\eta\mathit\;\mathit\cdot\mathit\;\mathit T}{\mathit2\mathit\;\mathit\cdot\mathit\;\mathit I}\mathit\;\mathit=\mathit\:\mathrm\pi\;\cdot\;\tan\left(\mathrm\delta\right)\) (22)
Dieses logarithmische Dekrement ist, wie Gleichung 22 [7, S. 43] [12] darstellt, direkt proportional zum Verlusttangens. Um sinnvoll damit umgehen zu können, muss die Periodendauer mit der Kreisfrequenz \(\omega\;=\:\frac{2\;\cdot\;\mathrm\pi}T\) bezeichnet werden und die Gleichung nach dem Verlusttangens aufgelöst werden:
\(\tan\left(\delta\right)\;=\:\frac\eta{I\:\cdot\;\omega}\) (23)
Anschaulich ist das logarithmische Dekrement als das logarithmische Verhältnis zweier aufeinanderfolgenden Amplituden \(φ_0\) und \(φ_1\) oder \(φ_1\) und \(φ_2\) beziehungsweise allgemein \(φ_n\) und \(φ_{n+1}\) definiert.
Siehe Formel (24)
Man sieht also, dass durch einfach physikalisch messbare Größen am Torsionspendel alle wesentlichen dynamisch- mechanischen Eigenschaften be- stimmt werden können. Somit eignet es sich sehr gut für die Zwecke, für die es im Rahmen dieser Arbeit gebraucht wird. Die Frequenzabhängigkeit ist dabei nicht unbedingt notwendig, da angenommen werden kann, dass die vorgenommenen Nachbehandlungen auf allen Frequenzbereichen ähnliche Effekte erzielen werden [7, S. 88 Grafik 3.20].
3.2 Aufbau des Torsionspendels
Das Torsionspendel besteht aus zwei Stäben, die an einer Grundplatte befestigt sind. Diese bilden eine Schiene für einen Schlitten, der vertikal an den Stäben verschoben werden und durch zwei Schrauben fixiert werden kann, um zu gewährleisten, dass die Höhe für jede Probe einzeln eingestellt werden kann. Somit können kleine Längenunterschiede ausgeglichen werden. An diesem Schlitten befindet sich die obere Aufnahme für die Probe. Das eigentliche Pendel besteht aus einer Halterung für das Torsionspendel, einem ferromagnetischen Eisenstab und einer gefrästen Schwungscheibe aus Aluminium. Die Halterung ist aus zwei Aluminiumplatten aufgebaut, die durch eine Schraubverbindung, das Torsionselement, mit dem Eisenstab verbinden. Die Schwungscheibe wird auf den Eisenstab aufgepresst und mit Schraubensicherung verklebt. Zudem befindet sich direkt unter dem Eisenstab ein Magnet, der den Stab ohne direkten Kontakt fixiert und somit unerwünschte Seitenschwingungen unterbindet, ohne die Dämpfung des Pendels zu erhöhen. Deswegen entsteht auch das Bedürfnis nach einer genauen Höhenkorrektur, da ohne diese die von dem Magneten aufgebrachte Kraft stark durch das unterschiedliche Spaltmaß variieren würde. Das gesamte Pendel ist in Eigenbau gefertigt geworden. Zur Messung wird die Lichtschranke des Cassy-Lab 2 seitlich über die Schwungscheibe geschoben. Die Schwungscheibe besitzt radiale Schlitze, über die die Zeiten zwischen den Verdunklungen gemessen werden. Die Lichtschranke wird über ein USB-Kabel und dem Cassy- Lab 2 mit dem Computer verbunden. Dabei wird die Timer-Box des Cassy-Lab benötigt. Um das Trägheitsmoment der Schwungscheibe zu bestimmen, wurde diese durch einen Zylinder modelliert, dessen Trägheitsmoment berechenbar ist. Von diesem wurden dann die Trägheitsmomente der acht Ausschnitte abgezogen. Dabei wurden diese durch Quader angenähert und der Steiner’sche Satz angewandt, da sie nicht um ihren Schwerpunkt rotieren. Das Trägheitsmoment der Stange und der Halterung ist vernachlässigbar. Man erhält den Wert von 2,08 ∙ 10–4 kg ∙ m2 für das Trägheitsmoment.
3.3 Beschreibung der Auswertungsmethode
Mit der Lichtschranke wird jeweils die Zeit für eine Dunkel- und Hellphase gemessen und die Zeit festgehalten, bei der dies stattgefunden hat. Dadurch kann die Winkelgeschwindigkeit als Funktion der Zeit dargestellt werden. An die gemessenen Werte wird die zugrundeliegende Funktion mittels der Methode der kleinsten Quadrate angepasst. Dabei handelt es sich bei der Funktion um den Betrag der Ableitung von Gleichung 17 mit einer Phasenverschiebung um den Winkel \(\)λ. Sie lautet:
Siehe Formel (25)
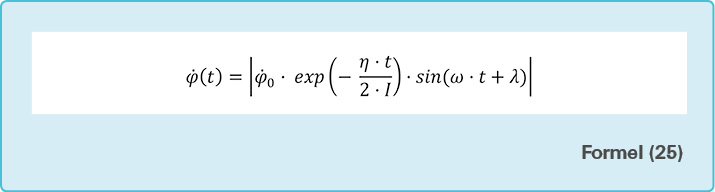
\(\overset.\varphi\left(t\right)\) ergibt sich aus dem Ableiten der Ursprungsfunktion:
Siehe Formel (26)

Für Näheres zur Zusammenfassung einer Summe aus Sinus- und Kosinusfunktion zu einer Winkelfunktion siehe „Analysis Teil 3“ [14].
Die FIT-Parameter der Funktion in den Excel-Tabellen sind dabei folgende Terme:
Siehe Formel (27)

Falls man die Winkelgeschwindigkeit durch das Formelzeichen \(ω\) repräsentiert, sieht die Formel (25) im Excel-Format folgendermaßen aus:
Siehe Formel (28)

Über die ermittelten Parameter für die jeweilige Messreihe können mittels der in 3.1 erarbeiteten Gleichungen die gesuchten Materialkennziffern wie Elastizitätsmodul, Viskositätsmodul und Verlusttangens automatisch errechnet werden [14].
3.4 Herstellung der Proben
Die Proben stammen allesamt aus der Lauffläche eines Michelin Wild Run’R. Dieser ist über das Online-Versandhaus Bike-Components erstanden worden. Der Reifen verfügt über eine dicke Lauffläche ohne Profil. Dadurch ist es möglich, dass man annähernd quadratische Stücke aus ihr herausschneidet. Dabei wird anfangs entlang der Mittellinie ein Schnitt mit der Schere gemacht und dann weitere Schnitte parallel dazu im Abstand von 4 mm, was auch der Dicke der Lauffläche entspricht. Die Probenstücke werden auf eine Länge von 15 mm gelängt.
Die Wahl fiel auf den Michelin Wild Run’R, bei dem durch die gaschromatographische Analyse Stoffe wie Schwefeldioxid nachgewiesen worden sind, die mit der Vulkanisation in Verbindung stehen. Dadurch steht fest, dass die Nachbehandlungen nach aufgeführtem Mechanismus stattfinden können. Auf eine gesonderte Entfernung der Karkasse von der Lauffläche wird verzichtet, da diese keine Auswirkungen auf den Vergleich hat und durch das Schneiden sowieso in höchstens 4 mm lange Stücke zerteilt worden ist. Dass die Veränderungen nur auf Veränderungen der Karkasse zurückzuführen sind, ist nicht wahrscheinlich, da die aus Aramidfasern bestehende Karkasse laut [15] chemisch sehr beständig gegen Essigsäure ist, sogar über einen Zeitraum von 120 Tagen. Die Aramidfasern sind zwar laut derselben Quelle angreifbar durch Schwefelsäure, aber erst ab einer Konzentration von 10 %, was bei der Nachbehandlung mit Natriumsulfit keineswegs der Fall ist, da nur minimale Mengen in der Größenordnung von 1 ml zugegeben worden sind. Außerdem werden die Proben vor der Messung durchgewalkt und verformt, damit keine Verfälschung des Ergebnisses durch den Payne-Effekt auftritt. Dieser Effekt, bei dem die ersten Deformationen unterschiedliche Kraftverläufe haben, lässt sich zum Beispiel durch das Aufbrechen des Füller-Füller- Netzwerks erklären [6].
3.5 Protokoll der Nachbehandlung
Die jeweils schon vor der Nachbehandlung gemessenen Proben werden zu Bündeln von jeweils drei zusammengefasst und individuell beschriftet. Zwei der drei Bündel werden in ein Reagenzglas gesteckt. Das erste Bündel wird mittels Essigsäure nachbehandelt. Dabei werden 30 ml Essigsäure mit einer Konzentration von 60 % mit 30 ml Wasser im Messzylinder auf eine Konzentration von 30 % verdünnt. Diese Lösung wird in das erste Reagenzglas geschüttet. Zu dem zweiten Reagenzglas wird eine wässrige mit wenigen Tropfen Schwefelsäure angesäuerte Natriumsulfitlösung gegeben, die im Becherglas mit einigen Spatelspitzen festem Natriumsulfit hergestellt worden ist. Im dritten Reagenzglas wird unter dem Abzug zunächst etwas Styrol in Aceton gelöst. Volumenmäßig beträgt das Mischungsverhältnis Styrol zu Aceton etwa 1 : 5. Dies findet unter dem Abzug statt, um Styrolemissionen abzuführen. Zu dieser Lösung wird das dritte Probenbündel gegeben und die radikalische Addition mit MEKP-Härter, der mit der Pipette zugegeben wird, initiiert. Alle Reaktionen finden bei Raumtemperatur und Umgebungsdruck statt. Nach ca. 48 Stunden werden die Proben den Lösungen entnommen. Die lange Dauer dient vor allem dazu, die Proben für das Torsionspendel nachweisbar nachzubehandeln, da nicht klar ist, wie schnell die Chemikalien in das Elastomer diffundieren. In der Praxis dürfte, wegen der hervorragenden Polymerisierbarkeit von Styrol [16], eine kürzere Zeit ausreichend sein, da die Deformationen, die bei der Haftreibung eine Rolle spielen, eine viel geringere Eindringtiefe haben. Dies wird im Versuchsaufbau auch in gewisser Weise berücksichtigt, da die Deformation der Gummiprobe im Torsionspendel außen größer als in der Mitte ist [13] und somit auch hier der am stärksten von der Nachbehandlung betroffene Bereich den größten Einfluss auf das Messergebnis nimmt. Die beiden ersten Probenbündel werden Probei der Entnahme noch mit Wasser abgespült und das Probenbündel aus dem Styrol mit Aceton gereinigt.
3.6 Protokoll der Messung
Die Messung der Proben erfolgt sowohl vor als auch nach der Nachbehandlung. Die individuelle Beschriftung erlaubt eine eindeutige Zuordnung der Messwerte für vorher und nachher. Die Proben werden der Reihe nach mithilfe der Werkzeuge in das Pendel mittels der Halterungen eingebaut. Dabei muss immer auch die Höhe des Schlittens nachjustiert werden, da die Proben nicht alle genau gleich lang sind. Deshalb muss auch individuell die Höhe nachgemessen werden. Es muss außerdem darauf geachtet werden, dass die Proben gerade eingespannt werden, da sonst eine zu große Unwucht auftritt. Danach wird das Pendel per Hand auf einige Umdrehungen ausgelenkt und beim Loslassen die Messung gestartet. Die Messwerte, die in der Software als Periodendauer bezeichnet werden, werden aufgezeichnet. Zu jeder Probe werden jeweils als Richtwert vier Messreihen vor und nach der Nachbehandlung angefertigt. Diese werden als Textdateien abgespeichert.
3.7 Statistische Auswertung
Aus jeder Messreihe wurde der Mittelwert \(\overline\chi\) gebildet. Dieser ergibt sich aus folgender Formel:
\(\overline\chi\;=\;\frac1N\;\cdot\;\sum_{i\;=\;1}^N\chi_i\)
Hierbei ist \(N\) die Anzahl der Einzelmessungen \(x_i\). Dabei ist zu beachten, dass dies analog für Elastizitätsmodul und Viskositätsmodul gemacht worden ist, das heißt \(x_i\) bezeichnet entweder eine Einzelmessung von Elastizitätsmodul oder Verlusttangens. Die Standardabweichung \(σ_M\) der Mittelwerte wurde über folgenden Ausdruck bestimmt [17].
\(\sigma_M\;=\:\frac1{\sqrt N}\;\cdot\;\sigma_E\)
Dabei ist \(σ_E\) die Standardabweichung der Einzelmessungen mit
\(\sigma_E\;=\:\sqrt{\frac1{N\:-\;1}\;\cdot\;{\textstyle\sum_{i\;=\:1\;}^N}\left(\overline x\;-\;x_i\right)^2}\)
Insgesamt ergibt sich daher:
\(\sigma_M\;=\:\frac1{\sqrt{N^2\;-\;N}}\;\cdot\;\sqrt{\sum_{i\;=\;1}^N\left(\overline x\;-\;x_i\right)^2}\)
Wegen der unterschiedlichen Probengeometrie konnte kein absoluter Vergleich durchgeführt werden. Das heißt, es musste eine relative Betrachtung durchgeführt werden. Hierbei wurde das Verhältnis \(\upsilon\) der Materialkennziffern von nachher \({\overline x}_n\) zu vorher \({\overline x}_v\) für eine Probe bestimmt. Dabei wurden jeweils die wahrscheinlichste Veränderung \(\upsilon_{mit}\), die maximale Veränderung \(\upsilon_{max}\) und die minimale Veränderung \(\upsilon_{min}\) wie folgt errechnet.
\(\upsilon_{mit}\;=\;\frac{{\overline x}_n}{{\overline x}_\nu}\)
\(\upsilon_{max}\;=\;\frac{{\overline x}_{n\;}+\;\sigma\;_M^n}{{\overline x}_\nu\;-\;\sigma\;_M^\nu}\)
\(\upsilon_{min}\;=\;\frac{{\overline x}_{n\;}-\;\sigma\;_M^n}{{\overline x}_\nu\;+\;\sigma\;_M^\nu}\)
Der Viskositätsmodul \(G''\) ist das Produkt aus Verlusttangens \(tan(δ)\) und Elastizitätsmodul \(G'\). Daraus folgt:
\(\upsilon_{G''}\;=\;\upsilon_{G'}\;\cdot\;\upsilon_{\tan(\delta)}\)
Unter der Berücksichtigung der Fehlerfortpflanzung kann der wahrscheinlichste Wert \(\nu_{G''}^{mit}\), der maximale Wert \(\nu_{G''}^{max}\) und der minimale Wert \(\nu_{G''}^{min}\) bestimmt werden.
\(\nu_{G''}^{mit}\;=\;\nu_{G'}^{mit}\;\cdot\;\nu_{\tan\left(\delta\right)}^{mit}\)
\(\nu_{G''}^{max}\;=\;\nu_{G'}^{max}\;\cdot\;\nu_{\tan\left(\delta\right)}^{max}\)
\(\nu_{G''}^{min}\;=\;\nu_{G'}^{min}\;\cdot\;\nu_{\tan\left(\delta\right)}^{min}\)
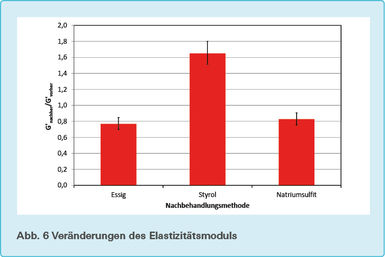
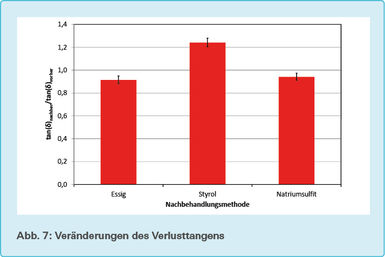
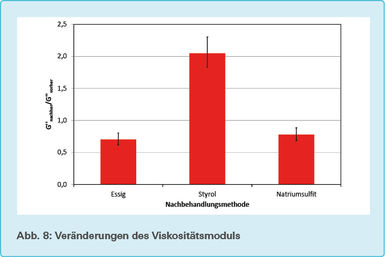
Diese drei Werte liegen nun für jede einzelne Probe vor. Um Aussagen über die Nachbehandlungsmethode zu machen, wurden diese Werte der drei Probeiben pro Nachbehandlungsmittel wieder gemittelt. In den Abb. 6 bis 8 ist die Höhe der Balken das mittlere Verhältnis, und das minimale und maximale Verhältnis wird durch die Fehlerbalken dargestellt.
3.8 Ergebnisse der Auswertung
Die Proben, die mit Essig nachbehandelt worden sind, zeigen eine deutliche Erniedrigung sowohl des Elastizitätsmoduls als auch des Verlusttangens. Dies heißt auch, dass der Viskositätsmodul kleiner geworden ist, da er das Produkt aus Elastizitätsmodul und Verlusttangens ist.
Bei der Nachbehandlung mit Styrol sind die umgekehrten Effekte aufgetreten. Während hier der Verlusttangens erhöht worden ist, ist auch der Elastizitätsmodul erhöht worden. Dies heißt auch, dass der Viskositätsmodul größer geworden ist, da er das Produkt aus Elastizitätsmodul und Verlusttangens ist.
Bei der Nachbehandlung mit Natriumsulfit zeigen sich ähnliche Effekte. Auch hier haben sich bei allen drei Proben Elastizitätsmodul und Verlusttangens erniedrigt. Dabei sind die Effekte ungefähr genauso groß wie bei der Nachbehandlung mit Essig. Daraus kann man folgern, dass der Viskositätsmodul umso kleiner geworden ist, da er das Produkt aus Elastizitätsmodul und Verlusttangens ist.
4.1 Fehleranalyse
Fehler können dadurch auftreten, dass man nur eine diskrete Messung mit der Lichtschranke anfertigt. Über die Periode kann die Winkelgeschwindigkeit für eine Achtelperiode ausgerechnet werden. In den Wendepunkten der Auslenkung ist es nicht möglich, festzustellen nach welcher Entfernung nach dem Einschnitt die Schwungscheibe die Rotationsrichtung ändert.
Nur für den Fall, dass sie genau nach der Hälfte des Weges die Rotationsrichtung ändert, stimmt der errechnete Wert für die Winkelgeschwindigkeit. Somit stimmen jeweils die Werte an den Wendepunkten nicht. Auf eine gesonderte Entfernung dieser Werte wird jedoch verzichtet, da diese kaum die errechnete Kreisfrequenz verändern und die Dämpfung über die maximalen Werte, nicht die minimalen, bestimmt wird.
Außerdem wurden nicht jegliche Seitenschwingungen unterbunden. Dadurch entstehen auch kleine Abweichungen bei der Messung. Aber auch diese dürften keine Rolle spielen, wenn nur Kreisfrequenz und Dämpfung bestimmt werden müssen.
Letztendlich muss auch anerkannt werden, dass das Pendel, wenn auch gering, eine Dämpfung abseits der Gummiprobe besitzt. Dies ist jedoch bei einem Vergleich der Werte von vorher und nachher nicht von Bedeutung. Die Dämpfung ist nicht linear abhängig von der momentanen Winkelgeschwindigkeit, sodass die Dämpfung geringfügig von Messreihe zu Messreihe variiert. Somit ist die Dämpfung vorher und nachher nicht exakt gleich, was den Vergleich beeinträchtigt, aber nicht groß ins Gewicht fallen dürfte.
Hinzu kommt, dass die Entfernung zum Magneten nicht absolut konstant über alle Messreihen ist, wodurch das Torsionselement nicht immer unter der gleichen Spannung steht, sodass auch hierdurch die Messung beeinträchtigt wird. Dies erwähnt auch Murayama [7].
Des Weiteren sind die Proben nicht exakt von gleicher Dicke, wodurch die Verdrillung sich nicht gleich verteilt. Auch dies könnte zu einer minimalen Verfälschung der verschiedenen Messreihen bei verschiedenen Ausgangsauslenkungen führen.
Die variierende Dicke führt auch zu den teils stark unterschiedlichen Werten für die Moduln über mehrere Proben hinweg. Die Dicke geht in Gleichung (20) in der vierten Potenz ein. Dies führt dazu, dass schwer messbare Schwankungen das Ergebnis stark beeinträchtigen. Trotzdem haben sie keine Auswirkungen auf den Vergleich.
4.2 Auswirkungen der Nachbehandlung mit Essig und Natriumsulfit
Die Nachbehandlungen mit Essig und Sulfit können gemeinsam besprochen werden, da die bei beiden Methoden hervorgerufenen Effekte sehr ähnlich sind. Dabei erscheinen diese beiden Nachbehandlungsmethoden weniger geeignet für eine Anwendung in der Praxis, da mit Essig und Sulfit eine Erniedrigung des Verlusttangens die Folge ist, was mit einer Erniedrigung der Hysteresekraft gleichzusetzen ist. Außerdem sinkt bei der Nachbehandlung mit Natriumsulfit und Essig der Viskositätsmodul, da sowohl Verlusttangens und Elastizitätsmodul sinken, was sich wiederum schlecht auf die Adhäsionskraft auswirkt. Letztendlich steigt auch der Abrollwiderstand, da der Reifen durch den kleineren Elastizitätsmodul stärker verformt wird und der dynamische Radius sich weiter vom eigentlichen Radius entfernt. Nur beim Walkwiderstand dürfte eine solche Nachbehandlung punkten, da der Reifen durch eine Erniedrigung des Verlusttangens elastischer geworden ist und somit mehr Deformationsenergie innerhalb eines Verformungszyklus wieder als nutzbare Energie freigegeben wird. Es kann also höchstens von einer spezifischen Nachbehandlung im Hinblick auf eine spezielle Situation gesprochen werden, da die potenziellen Verbesserungen beim Rollwiderstand kaum eine Rolle im Vergleich zu den Verschlechterungen bei den Reibkräften spielen. Außerdem müsste die Nachbehandlung nicht nur auf der Oberfläche angewandt werden, sondern auch tief in den Reifen eindringen.
VerDie Senkung des Elastizitätsmoduls bei der Nachbehandlung mit Natriumsulfit kann dadurch erklärt werden, dass der Vernetzungsgrad durch die Nachbehandlung gesenkt worden ist, da die Sulfidbrücken zu Thiolgruppen reduziert worden sind. Um dies zu testen, wurde die Nachbehandlung mit reinen Gummistücken aus demselben Reifen wiederholt. Diesmal wurde die Lösung mit Salzsäure angesäuert, dadurch kann jegliches gebildete Natriumsulfat nachgewiesen werden. Sollte Sulfat entstehen, bildet dies mit Bariumchlorid einen weißen Niederschlag [18]. Man sieht in Abb. 9, dass dies der Fall ist.
Es ist anzunehmen, dass diese Sulfatbildung tatsächlich durch die Reaktion mit den Schwefelbrücken entsteht, da sonst keine andere Erklärung bekannt ist.
Da aber auch der Verlusttangens gesenkt worden ist, kann man darauf schließen, dass der Viskositätsmodul noch stärker bei den jeweiligen Proben erniedrigt worden ist. Dies könnte man dadurch erklären, dass die Polymerketten sich ohne jegliche Quervernetzung unter Spannung energetisch sehr günstig anordnen können. Durch die Quervernetzung könnte es aber sein, dass sich Verwerfungen und Spannungen im Polymer bilden, die energetisch ungünstig sind. Die Energie, die nun hier bei der Deformation aufgewendet wird, wird als Wärme in der Relaxationsphase abgegeben, was heißt, dass der Viskositätsmodul größer geworden ist. Da man aber bei der Nachbehandlung diese Quervernetzung verringert, ist es möglich, dass sich das Polymer wieder energetisch günstiger im Vergleich zu vorher anordnen kann, was heißt, dass der Viskositätsmodul sinkt. Damit wird auch der Verlusttangens kleiner, da er das Verhältnis aus Viskositätsmodul zu Elastizitätsmodul ist, was beobachtet worden ist. Die in 2.2 erwähnte, von Murayama [7, S. 81 ff.] aufgestellte Verallgemeinerung widerspricht dieser Erklärung zwar, es dürfte sich aber um einen Spezialfall handeln, der von dieser Verallgemeinerung nicht erfasst wird.
4.3 Auswirkungen der Nachbehandlung mit Styrol
Bei der Nachbehandlung mit Styrol ist eine Erhöhung des Elastizitätsmoduls, des Viskositätsmoduls und des Verlusttangens beobachtet worden. Dieser Vorgang kann nicht mit dem in 2.2 erarbeiteten Modell von Polymeren erklärt werden. Eine Erhöhung des Verlusttangens wäre mit Gleichung (15) erwartet worden, falls nur die molare Masse erhöht worden wäre, da in diesem Fall der Elastizitätsmodul gesunken wäre und der Viskositätsmodul gleich geblieben oder größer geworden wäre, was in einem größeren Verlusttangens resultieren würde. Da aber der Elastizitätsmodul größer geworden ist, müssen andere Effekte, wie eine gesteigerte Quervernetzung, mit einbezogen werden. Laut Murayama [7, S. 81 ff.] korrespondiert aber eine Zunahme der molekularen Masse und Quervernetzung mit einer Abnahme der Dämpfung, und dies stellt einen Widerspruch zum beobachteten Ergebnis dar. Wegen dieser Widersprüche muss die richtige Antwort also aus einem Abwägen der Effekte resultieren oder es muss eine grundlegende Strukturveränderung angenommen werden.
Unter verschiedenen Gesichtspunkten eignet sich die Nachbehandlung mit Styrol besser als die Nachbehandlungen mit Natriumsulfit und Essig. Styrol führt mit der radikalischen Addition zu einer Erhärtung, sprich Vergrößerung, des Elastizitätsmoduls des Reifens, sodass der Abrollwiderstand, wenn auch nur geringfügig, kleiner wird, was durchaus positiv ist. Im Gegensatz dazu erhöht sich aber der Walkwiderstand, da durch die Erhöhung des Verlusttangens mehr Energie innerhalb eines Verformungszyklus als Wärme abgegeben wird. Aber da sowohl Verlusttangens als auch Viskositätsmodul steigen, werden Hysterese- und Adhäsionskraft größer, was beides positiv ist. Man kann also praktisch von einer allgemeingültigen Verbesserung sprechen, da fast keine Kompromisse eingegangen werden müssen. Außerdem ist zu beachten, dass Veränderungen durch die hier aufgeführte Nachbehandlung beim Rollwiderstand zwar vorhanden sind, aber kaum eine Rolle in der Praxis spielen, da Styrol vor allem als Oberflächennachbehandlungsmittel eingesetzt werden sollte. Deshalb scheint also die Nachbehandlung mit Styrol die beste in dieser Arbeit betrachtete Methode zu sein.
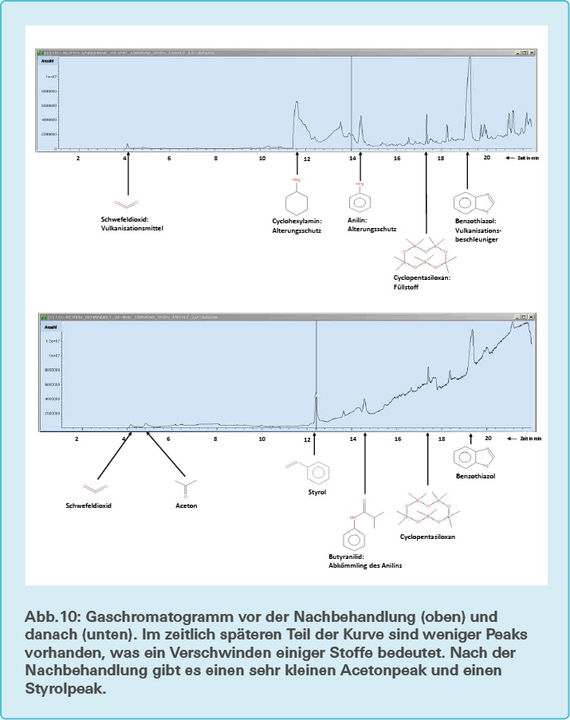
Um zu überprüfen, ob das Styrol tatsächlich an das Polymer bindet, ist eine Gaschromatographie mit gekoppelter Massenspektroskopie durchgeführt worden. Wie sich die chemische Zusammensetzung des Reifens durch die Nachbehandlung ändert, ist in der Abb.10 zu sehen.
Es ergeben sich verschiedene alternative Erklärungsmodelle für die Wirkung des Styrols. Im Folgenden werden verschieden Möglichkeiten aufgeführt und ihre Übereinstimmung mit den experimentellen Daten erläutert.
Eine erste mögliche Ursache könnte sein, dass bestimmte Substanzen, wie zum Beispiel Weichmacher, aus dem Polymer durch das Aceton herausgeschwemmt werden. Dies kommt in Betracht, da im hinteren Teil der Messkurve einige Peaks verschwinden und dies sich mit den physikalischen Veränderungen decken würde. Das Verschwinden des Cyclohexylaminpeaks dürfte dabei irrelevant sein, da dieses nicht als Weichmacher eingesetzt wird. Eine weitere mögliche Ursache ist, dass das Polymer durch das Aceton aufquillt. Als Ursache kann dies allerdings ausgeschlossen werden, da sehr wenig Aceton nach der Nachbehandlung nachgewiesen worden ist und dies nicht ausschlaggebend sein dürfte. Ebenfalls könnte das Polymer durch Monostyrol aufquellen. Dies erscheint wahrscheinlicher als das Aufquellen durch Aceton, da Styrol in größeren Mengen nachgewiesen worden ist. Andererseits hätte das Monostyrol, ähnlich wie Aceton, durch Verdampfen das Polymer verlassen müssen, da nur Polystyrol sich über den Zeitraum von knapp einem Jahr in dieser Menge im Polymer hätte halten können. Indirekt kann also gefolgert werden, dass sich das Styrol als Polystyrol im Polymer befinden muss. Es kann auch ausgeschlossen werden, dass das Styrol ohne an die Polymerketten zu binden im Elastomer ist, da dieses sich sonst bei knapp unter 300 °C am hinteren Ende der Messkurve zersetzen [16] und sofort verdampfen würde, was zu einem zweiten Styrolpeak führen würde. Dieser ist nicht vorhanden, weswegen die Polymerisation des Styrols an die Polymerketten als wahrscheinlichste Erklärung erscheint.
4.4 Aussagekraft und Nutzen der gewonnenen Ergebnisse
Wie genau sich die auftretenden Veränderungen auf das Fahren und die Reibung auswirken, kann experimentell nicht im Rahmen dieser Arbeit beantwortet werden. Von besonders großer Bedeutung ist hier auch die fehlende Messung über verschiedene Frequenzbereiche. Dennoch lassen die Arbeiten von Schramm [1] und Murayama [7] darauf schließen, dass es zu einer Verbesserung der Reibung und des Fahrverhaltens kommt. Der Autor ist bezüglich dieser Vorhersagen zuversichtlich. Wie groß auftretende Effekte tatsächlich sind, kann nicht bestimmt werden. Eine qualitative Aussage kann aber auf jeden Fall getroffen werden.
Es ist jedoch nachgewiesen worden, dass Erfolge, die mittels einer Nachbehandlung dieser Art erzielt worden sind, tatsächlich auf chemische Veränderungen zurückzuführen sind. Es kann ziemlich sicher ausgeschlossen werden, dass es sich nur um eine rein physikalische Nachbehandlung, also eine Reinigung der Oberfläche, handelt, da diese im Torsionspendel kaum erkennbar sein dürfte und durch die durchgeführten chemischen Tests auszuschließen ist. Außerdem ist die Nachbehandlung nicht ab Werk erhältlich und somit könnte es zu einem potenziellen Vorteil, sogar über das Niveau eines brandneuen durchentwickelten Reifens hinaus, kommen, da eine wie hier praktizierte Nachbehandlung der obersten Schicht wegen des Abriebes ständig erneuert werden müsste und dies vom Hersteller aus nicht möglich ist.
Diese Arbeit befasst sich mit der Verbesserung von verschiedenen Eigenschaften von Reifen. Diese Verbesserungen sollten dabei allein durch eine chemische Nachbehandlung des Reifens erzielt werden.
Aufgrund theoretischer Überlegungen sind zur Nachbehandlung Natriumsulfit und Styrol verwendet worden. Außerdem hat eine Nachbehandlung einiger Proben mit Essigsäure stattgefunden, da dies unter Radfahrern üblich ist. Zur Überprüfung der aufgestellten Thesen wurde ein selbstgebautes Torsionspendel verwendet. Die Messwerte wurden mittels Excel ausgewertet. Die Ergebnisse zeigen, dass die Nachbehandlungen mit Natriumsulfit und Essigsäure zu einer Reduzierung des Elastizitätsmoduls, des Verlusttangens und des Viskositätsmoduls führten. Die Nachbehandlung mit Styrol führte zu einer Erhöhung von Elastizitätsmodul, Verlusttangens und Viskositätsmodul.
Die Ergebnisse weisen nach, dass eine chemische Nachbehandlung tatsächlich eine Wirkung hat, wobei die Folgen für das Fahrverhalten der Reifen nicht genau bestätigt sind. Es gibt aber starke Hinweise darauf, dass diese wenigstens für qualitative Vorhersagen groß genug ist. Mit ziemlich großer Sicherheit kann ausgeschlossen werden, dass es sich nur um eine physikalische Reinigung handelt. Die Nachbehandlung mit dem Styrol erscheint am geeignetsten für eine Anwendung in der Praxis, wobei fast von einer allgemeingültigen Verbesserung gesprochen werden kann, da der Reifen sowohl einen besseren Rollwiderstand hat, der Radfahrer also seine Reibungsverluste durch den Reifen verringert, also mit weniger Kraftaufwand fahren kann, und er zugleich sicherer und schneller Abbremsen und Kurven fahren kann, da er über eine bessere Kraftübertragung auf die Straße verfügt. Die Nachbehandlungen mit Natriumsulfit und Essig scheinen höchstens als spezifische Nachbehandlung für spezielle Zwecke sinnvoll.
Die Nachbehandlungen haben das Potenzial, den Reifen über das Niveau eines komplett neuen Reifens zu heben, da eine Nachbehandlung der obersten Schichten von Seiten der Hersteller sehr unpraktikabel sein dürfte.
An dieser Stelle möchte ich mich bei all denjenigen bedanken, die mich während der Anfertigung dieser Arbeit unterstützt haben.
Zuerst gebührt mein Dank Barbara Menz, die mich auf Jugend forscht aufmerksam gemacht hat, mir sehr intensiv mit der Vorbereitung auf den Wettbewerb geholfen hat und für all meine Fragen zur Verfügung stand.
Ebenfalls möchte ich mich bei Elmar Daubenmerkl bedanken, der mir im Rahmen des W-Seminars „Material, Funktion und Design – Das Fahrrad des 21. Jahrhunderts“ das Verfassen der vorliegenden Arbeit ermöglicht hat und bei Messungen und Nachbehandlungen helfend zur Seite stand.
Außerdem möchte ich mich bei zwei weiteren Lehrern des Albertus-Magnus-Gymnasiums bedanken:
Stefanie Vogl und Andrea Wagner. Ohne Sie wäre ich nicht dazu in der Lage gewesen, die Gerätschaften in der Physiksammlung zu benutzen.
Zudem wäre die Erstellung des Gaschromatogramms ohne die Hilfe von Josef Steiner von der Infineon Technologies AG nicht möglich gewesen. Herzlichsten Dank an dieser Stelle!
Last but not least gebührt Uli Herwanger, Jugend forscht Bayern, und Hans Jörg-Zeller von der Continental AG für das Mentoring zum Bundeswettbewerb besonderer Dank.
1] E. J. Schramm, Reibung von Elastomeren auf rauen Oberflächen und Beschreibung von Nassbremseigenschaften von PKW-Reifen, Universität Regensburg, 2002.
[2] M. Gressmann, Fahrradphysik und Biomechanik, Kiel: Moby-Dick-Verlag, 2009.
[3] PW3 Elastizität/Trägheitsmoment, Universität Wien.
[4] F. P. Beer und E. R. Johnston, Jr., Mechanics of Materials, United States of America: McGraw- Hill, Inc., 1981.
[5] Polymerservice Merseburg, „Entropieelastizität,“ [Online]. URL: http://wiki.polymerservice-merseburg.de/index.php/Entropieelastizit%C3%A4t (Letzter Zugriff: 13.05.2016).
[6] J. Böhm, Der Payneeffekt: Interpretation und Anwendung in einem neuen Materialgesetz für Elastomere, Universität Regensburg, 2001.
[7] T. Murayama, dynamic mechanical analysis of polymeric materials, Amsterdam-Oxford-New York: Elsevier publishing company, 1978.
[8] Michelin, „Kautschukmischung und Reifenkarkasse auf Basis derselben“. Patent EP0680998A1, 1994 [Stand: 13.05.2016].
[9] Chemgapedia, „Schwefelvulkanisation von Kautschuk,“ [Online]. URL: http://www.chemgapedia.de/vsengine/vlu/vsc/de/ch/9/mac/netzwerke/vulkan/schwefel.vlu/Page/vsc/de/ch/9/mac/netzwerke/vulkan/schwefein.vscml.html (Letzter Zugriff: 13.05.2016).
[10] Wikiwand, „Styrol-Butadien-Kautschuk,“ [Online]. URL: http://www.wikiwand.com/de/Styrol-Butadien-Kautschuk (Letzter Zugriff: 13.05.2016).
[11] M. Graf, Polarmodififkation von Butadienkautschuk mit Polyethylenglykol, Universität Bayreuth, 2002.
[12] T. Raab und M. Seidling, Praktikumsbericht: Torsionsoszillator, 2012.
[13] T. Preußler, Torsion, Umwelt-Campus Birkenfeld: Fachhochschule Trier.
[14] Niedersächsischer Bildungsserver, „Analysis Teil 3: trigonometrische Funktionen,“ [Online]. URL: http://nibis.ni.schule.de/~lbs-gym/AnalysisTeil3pdf/trigFunktionen.pdf (Letzter Zugriff: 26.07.2016).
[15] M. Flemming, S. Roth und G. Ziegmann, Faserverbundweisen: Fasern und Matrices, Heidelberg: Springer verlag Berlin Heidelberg, 1995.
[16] Wikipedia, „Styrol,“ [Online]. URL: https://de.wikipedia.org/wiki/Styrol (Letzter Zugriff: 18.03.2018).
[17] R. Dinter, Fehlerrechnung für Einsteiger, Hamburg: Institut für angewandte Physik, Universität Hamburg, Februar 2011.
[18] Seilnacht, „Bariumchlorid,“ [Online]. URL: http://www.seilnacht.com/Chemie/ch_bacl2.htm (Letzter Zugriff: 23.02.2018).