Radiowellen aus dem All
Das All hat uns viel mitzuteilen. Die Radioastronomie bietet einen guten Zugang zu Informationen über Ereignisse, die in Entfernungen jenseits der irdischen Größenverhältnisse stattfinden. In dieser Arbeit wurde die Milchstraße mittels Langzeitmessungen vermessen. Die verwendete Messapparatur bestand aus einem Callisto-Radiospektrometer und einer LWA-Antenne.
Als Radioastronomie wird dasjenige Teilgebiet der Astronomie bezeichnet, welches astronomische Objekte anhand der von ihnen emittierten Radiowellen untersucht. Radiowellen umfassen alle Wellen des elektromagnetischen Spektrums, deren Frequenz zwischen einigen Kilohertz und drei Gigahertz liegt. Wichtige astronomische Radioquellen sind die Sonne, Planeten und Monde, Radiogalaxien, Quasare, Pulsare und Supernova- Überreste [1]. In dieser Arbeit wurden die Radioemissionen der Milchstraße vermessen. Diese ist hauptsächlich Synchrotronstrahlung, welche entsteht, wenn sich geladene Teilchen in Kreisbahnen um Magnetfelder bewegen. Dieser Mechanismus findet im interstellaren Raum statt, wo Elektronen der kosmischen Strahlung an Supernova-Stoßwellen auf beinahe Lichtgeschwindigkeit beschleunigt werden.
Ihre Anfänge nahm die Radioastronomie im Jahr 1931, als Karl Guthe Jansky, ein Radioingenieur der Bell Telephone Laboratories in New Jersey, den Auftrag erhielt, eine unbekannte Rauschquelle im Bereich von 20 MHz zu determinieren. Hierzu baute er eine steuerbare Antenne, mit der er die Richtung der Störquelle ausmachen konnte. Zu seinem Erstaunen fand er heraus, dass die Störung extraterrestrischen Ursprungs war. Seine Publikationen wurden anfangs von den meisten Astronomen als irrelevant wahrgenommen. Zuerst lag die Vermutung darin, dass die Quelle dieser Strahlung die Sonne ist, da ein 24-Stunden-Rhythmus zu erkennen war. Längere Beobachtungen zeigten, dass die Periode kleiner war und es sich in Wirklichkeit um Radioemissionen der Milchstraße und anderer Radioquellen, wie der Radiogalaxie Cygnus A und der Supernova-Überreste Cassiopeia A, handelte [2].
Dieses Pionierexperiment wurde in dieser Arbeit mit einfachen und erschwinglichen Mitteln rekonstruiert. Die gewonnenen Daten wurden auf die Periodizität untersucht, um andere Radioquellen auszuschließen. Zudem wurden anhand einer Simulation verschiedene Modelle der Form der Milchstrasse im Radiobereich erstellt.
Die LWA-Antenne, die in dieser Arbeit zum Einsatz kam, wurde vom astronomischen Institut der ETH-Zürich zur Verfügung gestellt. LWA steht für „Long Wavelength Array“, was ein Radioteleskop in New Mexiko ist, das momentan aus mehreren hundert LWA-Antennen besteht und noch ausgebaut werden soll. Wie der Name schon sagt, ist die Antenne für langwellige Radiowellen ausgelegt, also niedrige Frequenzen des Radiospektrums. Konkret umfasst das messbare Spektrum den Bereich von 5 MHz bis 100 MHz. Die Antenne besteht aus zwei Dipolen, die in einem rechten Winkel zueinander stehen. Somit können über die beiden Dipole unterschiedliche Polarisationen (vgl. Abb. 1) gemessen werden. Zudem sind die einzelnen Pole 45° zur Senkrechten nach unten geknickt, was zur wesentlichen Richtcharakteristik der Antenne beiträgt. Die Dipole ähneln den Schmetterlingsantennen, wobei sie vom Mittelpunkt aus nach außen breiter werden und somit die messbare Bandbreite erhöhen.
Die Richtwirkung der LWA-Antenne kann in der horizontalen und in der vertikalen Ebene beschrieben werden. In der horizontalen Ebene hat sie weitgehend die Charakteristik eines isotropen Strahlers. In der vertikalen nimmt die Empfangsleistung jedoch in niedrigen Höhenwinkeln ab (vgl. Abb. 2) Zudem zeigt sich eine Abhängigkeit der Richtcharakteristik von der Frequenz und der Polarisation der Wellen. Für diese Arbeit ist nur die wesentliche Charakteristik um 50 MHz beim Empfang von unpolarisierter Strahlung von Interesse [3].
Der Callisto-Empfänger wurde von der ehemaligen Gruppe für Radio- und Plasmaphysik der ETH Zürich entwickelt. Sein Anwendungsgebiet hat der Callisto vorwiegend in der solaren Radiospektrometrie und in der Messung von Funkbelastung und dient weltweit der Forschung und Bildung. Der Empfänger baut auf dem Prinzip der heterodynen Detektion auf, was heißt, dass die einzelnen Frequenzen durch Mischung mit Referenzfrequenzen detektiert werden. Das Hauptstück der Hardware ist ein Breitband-Kabelfernseh-Tuner, welcher in Frequenzen zwischen 45 MHz und 870 MHz arbeitet und eine Auflösung von 62,5 kHz hat. Es können bis zu 800 Messungen pro Sekunde gemacht werden, wobei die Daten über ein RS232-Kabel an den Rechner gelangen und als FITS-Dateien [4] (Flexible Interchange Transport System) abgespeichert werden [5].
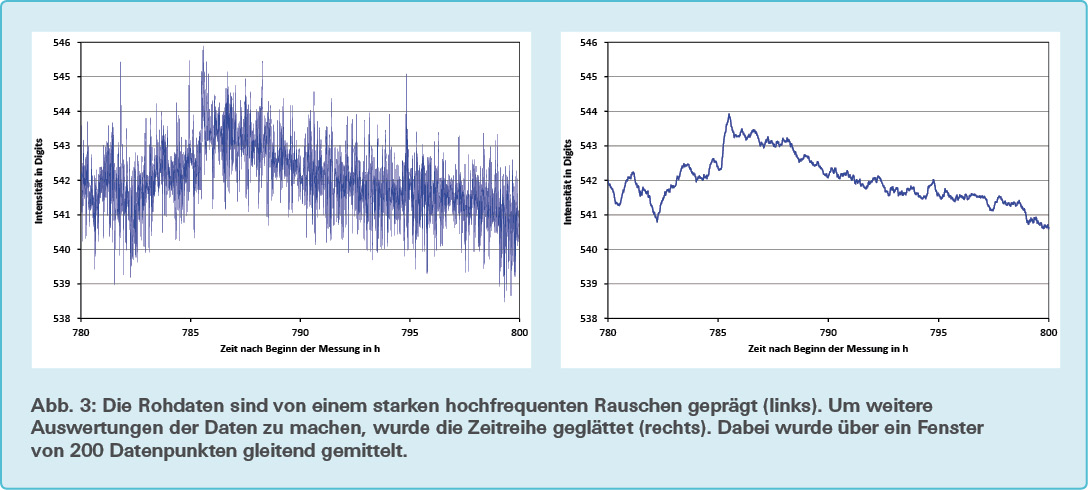
Da die Intensitäten der Radioemissionen der Milchstraße mit abnehmender Wellenlänge schwächer und mit zunehmender Wellenlänge stärker von der Ionosphäre reflektiert werden, war die ideale Frequenz einer terrestrischen Messung unbekannt. Außerdem kommt es darauf an, auf welche Frequenz das Radioteleskop am sensibelsten reagiert. Erste Versuche zeigten, dass tiefe Frequenzen heftiger gestört sind, woraus schwach ausgeprägte Signalpeaks beim Transit der Milchstraße resultieren. Aus diesem Grund wurden fünf ungestörte Frequenzen zwischen 45 MHz und 50 MHz selektiert, die während des Messvorgangs aufgezeichnet wurden, wobei die spektrale Auflösung 62,5 kHz betrug (vgl. Empfänger). Da der gemessene Prozess beinahe einen ganzen Tag dauert, kann der Callisto-Empfänger so konfiguriert werden, dass 100 MessMesspunkte gemittelt werden. Das entspricht 25 Sekunden pro Datenpunkt, wenn der Callisto mit vier Messungen pro Sekunde konfiguriert wurde. Insgesamt wurde 39 Tage lang ununterbrochen gemessen. Die gesamte Datenverarbeitung wurde aufgrund der großen Anzahl an Datenpunkten mit einem selbst erstellten C++-Programm gemacht. Da die Zeitreihe durchgehend von hochfrequentem Rauschen gestört ist, wurde ein digitaler Tiefpassfilter programmiert. Hierzu eignet sich die Methode des gleitenden Mittelwerts. Dabei wird ein Datenpunkt mit einer bestimmten Anzahl benachbarter Datenpunkte gemittelt, was eine Glättung des Messsignals zur Folge hat (vgl. Abb. 3).
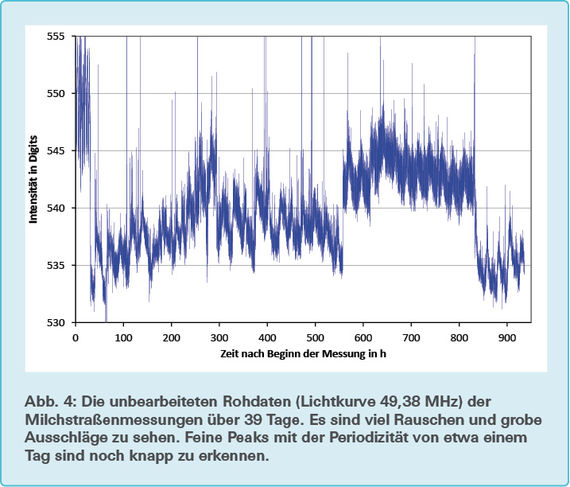
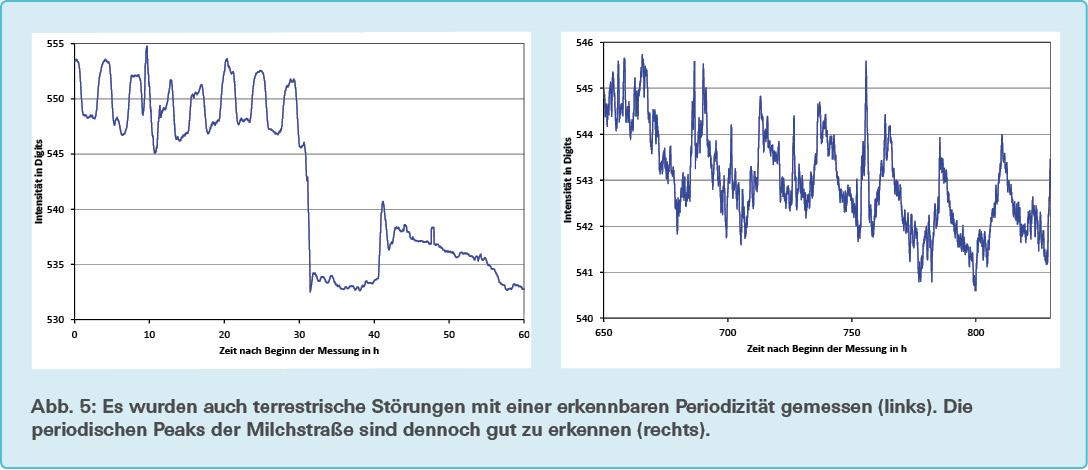
Obwohl die fünf ungestörtesten Frequenzen für die Messungen gewählt wurden, sind erheblich viele Störungen zu erkennen (vgl. Abb. 4). Gewisse Störungen sind frequenzübergreifend und über mehrere Tage vorhanden. Dazu gehören abrupte Signalhebungen und Signalabfälle, die das Signal für einige Minuten bis zu mehreren Tagen auf der gleichen Signalstärke erhalten haben. Der erste Tag der Messung ist durch eine Störung mit ausgeprägter Periodizität gekennzeichnet (vgl. Abb. 5), was darauf hinweist, dass es sich um eine terrestrische Störquelle handelt. Ihre Periodizität beträgt 4,08 ± 0,17 h und ist in der Frequenz 49,38 MHz am deutlichsten zu erkennen. Die Ursache dieser Störung ist nicht bekannt. Weitere Störungen sind sehr starke Peaks eines oder weniger Messpunkte. Solche Peaks sind auf Blitze und Solar Radio Bursts zurückzuführen. Zwischen 200 und 300 Stunden nach Messbeginn ist ein leichter Anstieg der gesamten Kurve zu sehen und zwischen 550 und 850 Stunden ist das gesamte Signal im Vergleich zum Rest der Lichtkurve etwas angehoben. Störungen dieser Art sind wahrscheinlich mit Wackelkontakten oder Feuchtigkeit in Steckverbindern in Verbindung zu bringen. Es konnte nicht herausgefunden werden, wodurch diese Störungen verursacht wurden.
Trotz der häufigen Störungen sind in allen Frequenzen über fast alle Tage Peaks mit einer Periode von etwa einem Tag zu erkennen. Somit kann die Periodizität der Peaks zwar gut ermittelt werden, allerdings ist das Mitteln der einzelnen Kurven schwierig, da sich ihre Amplitude und ihr Offset teilweise stark unterscheiden. Brauchbare aneinanderhängende und gleichartige Kurven sind zwischen 650 und 850, wie auch zwischen 850 und 950 Stunden nach Messbeginn zu finden (vgl. Abb. 5).
Um die Zeitreihe auf die Periodizität zu untersuchen, kommen zwei Methoden in Frage. Die erste und einfachste Methode ist, die zeitliche Verschiebung der Peaks über mehrere Tage zu betrachten. Dazu wird die Differenz von zwei möglichst weit auseinanderliegenden eindeutigen Peaks durch die Anzahl dazwischenliegender Perioden dividiert. Die zweite Methode ist die Fouriertransformation, welche eine Funktion der Zeit in eine Funktion der Frequenz umwandelt. Dies beruht auf der Theorie, dass jede beliebige Funktion aus Sinusund Cosinus-Funktionen rekonstruiert werden kann. Der im Programm verwendete Algorithmus ist eine Fast-Fourier- Transformation von Numerical Recipies in C (NRC) [7].
Das Resultat der über 33 Perioden errechneten Periodizität anhand der ersten Methode ist 23,91 ± 0,06 h. Die Sonne sowie terrestrische Quellen sind auszuschließen, da der 24-Stundenrhythmus nicht im Bereich der Fehlerbegrenzungen liegt. Der siderische Tag liegt mit 23,93 h nur 72 Sekunden daneben und befindet sich noch innerhalb des Schätzfehlers. Somit muss es sich bei der gemessenen Strahlungsquelle um eine extrasolare Radioquelle handeln. Eine unterstützende Evidenz dafür, dass es sich dabei um Radioemissionen der Milchstraße handelt, bietet die Simulation der Galaxiensignale (vgl. Simulation).
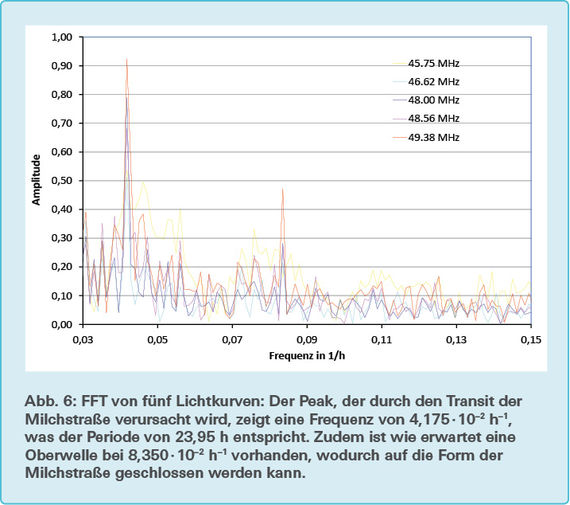
Das Resultat der Fast-Fourier-Transformation hat unter anderem frequenzübergreifend eine Frequenz von (4,175 ± 0,055) · 10–2 h–1 ergeben (vgl. Abb. 6), was einer Periodizität von 23,95 ± 0,12 h entspricht. Somit können die Sonne und terrestrische Strahlungsquellen nicht vollständig ausgeschlossen werden, da die geschätzten Fehlergrenzen die 24-Stunden-Periode noch beinhalten. Trotzdem besteht wenig Zweifel, dass dies der gesuchte Peak ist, da es der einzige ist, welcher einer extrasolaren Radioquelle zugeordnet werden könnte, weil es ziemlich genau der Periodizität eines siderischen Tages entspricht. Ein weiterer interessanter Peak befindet sich bei der Frequenz (8,350 ± 0,055) · 10–2 h–1, was genau dem Doppelten der Frequenz des ersten Peaks entspricht. Dies deutet darauf hin, dass es sich um eine Oberwelle der gemessenen Milchstraßenfunktion handelt. Denn die Funktion der gemessenen Milchstraße gleicht nicht einer Gaußfunktion, wie es bei einer Punktquelle sein müsste. Die gemessene Funktion entspricht näherungsweise der Faltung einer Gaußfunktion mit einer Rechteckoder Ellipsenfunktion (vgl. Simulation). Die resultierende Form gleicht eher einem schiefen Dreieck, was der Grund dafür ist, dass im Fourierspektrum neben der Grundfrequenz auch Oberfrequenzen auftreten müssen. Das stimmt mit der beobachteten ersten Oberfrequenz im experimentellen Fourierspektrum überein.
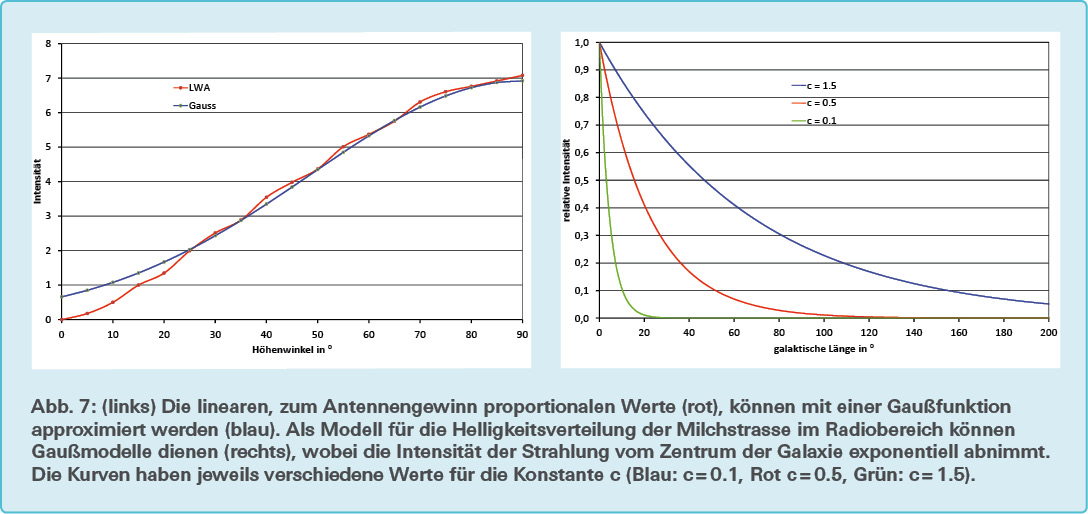
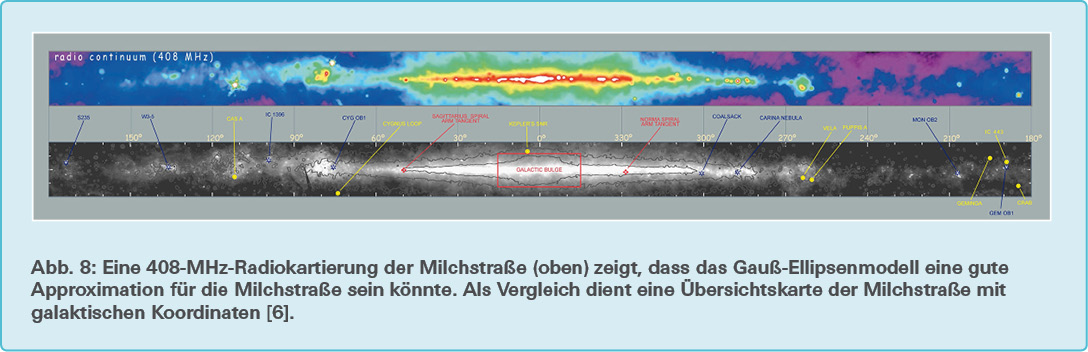
Die wesentliche Form der Galaxiensignale ist im Gegensatz zum Signal einer punktförmigen Quelle nicht nur von der Richtcharakteristik der Antenne, sondern auch von der Form der Milchstraße im Radiobereich abhängig. Die Galaxiensignale können weiter untersucht werden, indem ein Modell für die Milchstraße angenommen wird. In dieser Simulation wurden drei verschiedene Galaxienmodelle untersucht. Im ersten Modell wird die Galaxis als in galaktischen Koordinaten rechteckige Fläche angenommen. Im zweiten und im dritten Modell ist die Form der Galaxis in galaktischen Koordinaten elliptisch. Während beim Rechteck- und beim gewöhnlichen Ellipsenmodell die Helligkeit über die ganze Fläche hinweg homogen ist, kann die Helligkeit B(λ,β) eines Punktes im Gauß-Ellipsenmodell mit der Formel \(B \big( \lambda . \beta \big)= e - \begin{pmatrix}\big( \frac{ \lambda }{a} \big) ^2 + \big(\frac{ \beta }{b})^2 \\ c \end{pmatrix}\) beschrieben werden (vgl. Abb. 7). Dabei ist λ die galaktische Länge, β die galaktische Breite, a die Länge und b die Breite der Hauptachsen einer Ellipse. Mittels der positiven Konstante c kann das Maß der exponentiellen Abnahme bestimmt werden. Für die Bestimmung der Länge der Hauptachsen wurde eine 408-MHz-Radiokartierung der Milchstraße zu Hilfe genommen. Für die Länge a wurde der Wert 50° und für die Breite b der Wert 5° gewählt (vgl. Abb. 8).
Die LWA-Antenne ist in der horizontalen Ebene näherungsweise isotrop, wodurch die Empfangsstärke nur vom Höhenwinkel abhängig ist (vgl. Messapparatur). Dabei können die aus dem Richtdiagramm der LWA-Antenne entnommenen Dezibel-Werte des Antennengewinns G(h) in lineare umgerechnet und mit der Gaußfunktion \(G \big(h\big) = \frac{720}{ \sqrt{2 \pi \cdot 42,5^2} } \cdot e ^{- \frac{1}{2} \big( \frac{h-90 ^ \circ} {42,5} \big)^2}\) angenähert werden (vgl. Abb. 7). Da die Helligkeitsfunktion der Milchstraße und die Gewinnfunktion der Antenne von zwei unterschiedlichen Koordinatensystemen, dem galaktischen und dem horizontalen, abhängig sind, können diese noch nicht sinnvoll miteinander integriert werden. Deshalb müssen die horizontalen Koordinaten mit den in der sphärischen Astronomie bekannten Koordinatentransformationen in galaktische Koordinaten umgewandelt werden. Danach kann das resultierende Signal s(t) als Integral der Helligkeitsfunktion der Milchstraße mit der Gewichtung der Gaußfunktion der LWA-Antenne beschrieben werden, was dem doppelten Integral (s. Formel 3) entspricht. Der Raumwinkel dΩ kann in die Komponente des Azimuts dA und des Höhenwinkels dh ∙ cos(h) zerlegt werden. Numerisch kann dieses Doppelintegral mit der Doppelsumme (s. Formel 4) approximiert werden. Es muss beachtet werden, dass die Helligkeitsfunktion der Galaxie von der Zeit abhängig ist und dass die Simulation Echtzeitdaten ausgibt.
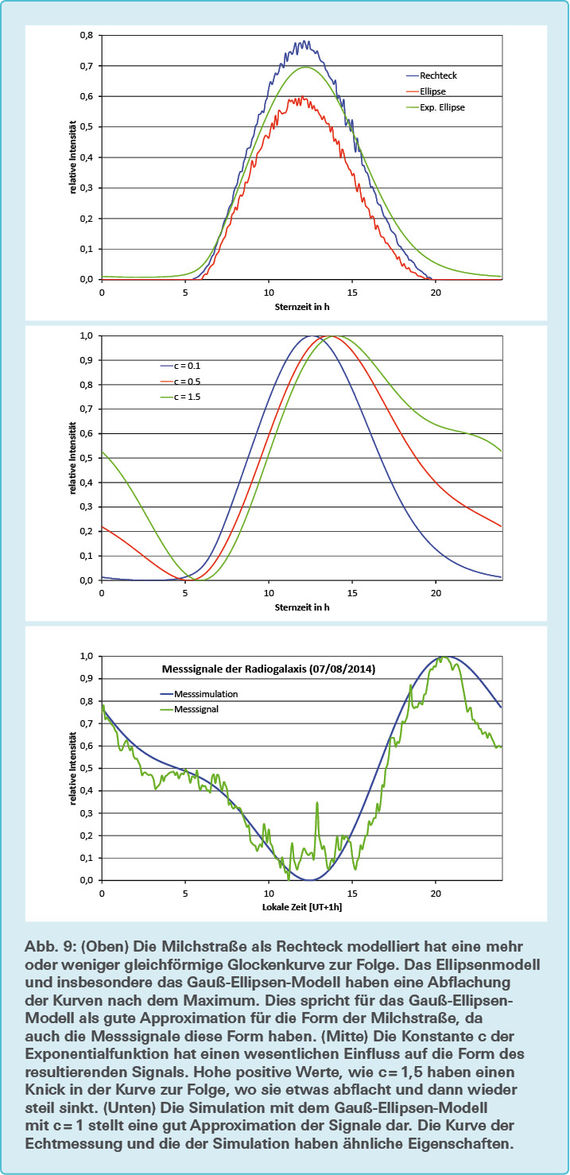
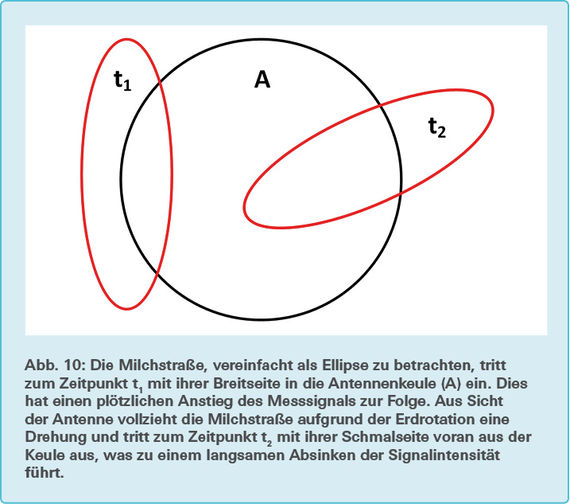
Die Simulation mit einem Rechteckmodell hat als Lichtkurve eine ziemlich gleichförmige Glockenkurve ergeben (vgl. Abb. 9). Bei den Ellipsenmodellen hingegen ist klar zu sehen, dass die Lichtkurve anfangs stark steigt und nach dem Peak flach sinkt. Besonders stark ist dies beim Gauß-Ellipsen-Modell zu erkennen, wobei tiefere positive Werte für die Konstante c der Exponentialfunktion einen umso flacheren Abgang der Kurve zur Folge haben. Für c = 1,5 ist sogar ein Knick im Abgang der Kurve zu sehen, wo sie abflacht und dann wieder etwas steiler sinkt. Dies macht deutlich, dass von den drei verwendeten Modellen das Gauß-Ellipsen- Modell die beste Approximation für die Form der Milchstraße ist. Die Abflachung der Kurve kann dadurch erklärt werden, dass die Galaxienellipse aus Sicht der Antennenkeule aufgrund der Erdrotation eine Drehung macht und bei der Austrittsphase länger in der Antennenkeule verbleibt (vgl. Abb. 10). Um die simulierten Signale mit den gemessenen zu vergleichen, wurden alle Sterntage der Frequenz 49,38 MHz miteinander gemittelt. Die Mittelung entspricht einer Messung vom 07/08/2014, deren Datum auch Ausgangspunkt für die Simulation war. Für die Konstante c der Exponentialfunktion wurde der Wert 1 gewählt. Die Signale der Simulation wie auch die Messsignale sinken anfangs mit einer ähnlichen Steigung. Beide Signale flachen bei etwa 4 h ab, wobei diese Abflachung sich beim simulierten Signal um etwa 10 h wieder aufhebt. Obwohl beide Kurven zu selben Zeitpunkten ihre Extremalpunkte haben, steigt das simulierte Signal anfangs stärker als das Messsignal. Somit ist die Abflachung des simulierten Signals beim Maximum größer als die des Messsignals. Dasselbe ist auch beim Absinken zu sehen. Der Grund für die Differenzen zwischen Simulation und Echtmessung liegen darin, dass in der Simulation Modelle verwendet werden, welche die Komplexität der wahren Form der Milchstraße nur approximieren. Zudem sind auch von Seiten der Messsignale Fehler zu erwarten, welche durch terrestrische Störungen und Ungenauigkeiten der Messapparatur entstehen. Starke Radioquellen wie Cygnus A und Cassiopeia A wurden in der Simulation nicht einbezogen. Allerdings wurde auch kein Zusammenhang zwischen dem gemessenen Signal und der Kulmination dieser Quellen festgestellt. Der Signalpeak koinzidiert jedoch mit der Kulmination unseres galaktischen Zentrums. Da das gemessene Signal für eine Flächenquelle spricht und die zuvor genannten Quellen als Punktquellen approximiert werden können, muss es sich bei den gemessenen Signalen um Radioemissionen der Milchstraße handeln. Die emittierte Strahlung ist breitbandig und tendiert dazu, in tieferen Frequenzen intensiver zu werden. Die Koinzidenz des Signalpeaks mit der Kulmination des galaktischen Zentrums kann dadurch erklärt werden, dass das Maximum dieser Synchrotronstrahlung im interstellaren Medium mit dem galaktischen Zentrum zusammenfällt.
Die Simulation scheint die Messkurve mit einer recht hohen Genauigkeit wiederzugeben, was dafür spricht, dass ein Gauß-Ellipsen-Modell eine gute Approximation für die Form der Milchstraßenscheibe ist. Dass die Extremalpunkte der beiden Kurven zusammentreffen, spricht ebenfalls für die Genauigkeit des Programms und ihrer Modelle.
In dieser Arbeit wurde ein verhältnismäßig kostengünstiges Radioteleskop mit einer LWA-Antenne und einem Callisto-Empfänger in Betrieb genommen. Die Milchstraße konnte anhand der Ermittlung der Periodizität mittels unterschiedlicher Methoden nachgewiesen werden. Die Zeitreihe könnte weiter bearbeitet werden, indem Hoch- und Tiefpassfilter in der Rekonstruktion der Fouriertransformierten eingebaut werden und die einzelnen Perioden auf die gleiche Amplitude normiert werden. Somit könnten die Perioden miteinander gemittelt werden, um die Form der Milchstraßenfunktion zu approximieren. Eine Simulation der Galaxiensignale konnte aufzeigen, warum die gemessenen Signale keine gleichmäßige Form haben. Aus messtechnischer Sicht eignet sich die LWA-Antenne gut für Messungen dieser Art, da sie eine schwache Richtcharakteristik aufweist. Somit kann auch das galaktische Zentrum trotz der am Messstandort niedrigen Kulmination von etwa 15° gut gemessen werden.
Radioastronomie ist eine Wissenschaft, die das Wissen von diversen physikalischen Teilbereichen erfordert. Dazu gehören die Hochfrequenztechnik, Kommunikationstechnik, Astronomie und natürlich auch physikalische und mathematische Grundlagen. Somit war ich auf die Hilfe mehrerer Personen angewiesen, die mir mit ihrem großen Hintergrundwissen den richtigen Weg weisen konnten. Als erstes möchte ich mich bei Dr. Rolf Heeb bedanken, der mir als Hauptbetreuer der Arbeit vor allem mit den physikalischen und mathematischen Grundlagen wie auch mit diversen Datenverarbeitungsmethoden helfen konnte. Einen ganz besonderen Dank möchte ich Christian Monstein vom Institut für Astronomie der ETH Zürich aussprechen. Als Hauptverantwortlicher der Callisto-Community konnte er mir viel seines Hintergrundwissens im Bereich praktischer und theoretischer Radioastronomie vermitteln und mir Ratschläge zu Literatur geben. Ebenfalls hat er mir den Zugang zu diversem Material der ETH, aber auch zu persönlichem Material ermöglicht. Im Rahmen des Nationalen Wettbewerbs von „Schweizer Jugend Forscht“ wurde mir Prof. Dr. Arnold Benz als Experte zugeteilt. Auch ihm möchte ich für seine Unterstützung danken. Christian Bircher möchte ich für den Zugang zu Material der Kantonsschule Wattwil sowie für die Anschaffung von neuem Material danken. Als Physikassistent der Kantonsschule Wattwil leistete er stets kompetente Hilfe bei der Bewältigung von technischen Problemen.
- [1] Vuscina, R., Grundlagen der Radioastronomie – vom Radar bis hin zum weltweiten Netz von Radioteleskopen, (März 2009), http://www.mpifr-bonn.mpg.de/412925/michael_hamm, (Zugriff am 15. September 2016).
- [2] Fielding, J., Amateur Radio Astronomy, Radio Society of Great Britain, (2006).
- [3] Reeve, W.D., Modeling the Long Wavelength Array Corossed-Dipole Antenna, (08. Februar 2014), http://www.reeve.com/Documents/Long%20Wavelength%20Array/Reeve_LWA-Model.pdf, (Zugriff am 19. Februar 2014).
- [4] International Astronomical Union FITS Working Group, Definition of the Flexible Image Trasport System (FITS), http://fits.gsfc.nasa.gov/standard40/fits_standard-40draft1.pdf, (Zugriff am 31.08.2016).
- [5] Monstein, C., e-Callisto Operating Manual, (23. Oktober 2006), http://e-callisto.org/Software/eCallistoManual.pdf, (Zugriff am 03. Mai 2014).
- [6] Myers, J. D., Multy Wavelength Milky Way, http://mwmw.gsfc.nasa.gov/mmw_images.html, (Zugriff am 14. März 2015).
- [7] Press, W. H., Teukolsky, S. A., Vetterling, W. T., Flannery, B. P., Numerical Recipes in C – The Art of Scientific Computing, 2nd Edition, Cambridge University Press (1995).